Contents

A common problem for machine learning models is overfitting, we describe several techniques to mitigate this issue.

To mitigate overfitting, we can apply a number of techniques such as the following:

Regularization
Cross-validation
Feature reduction

Overfitting

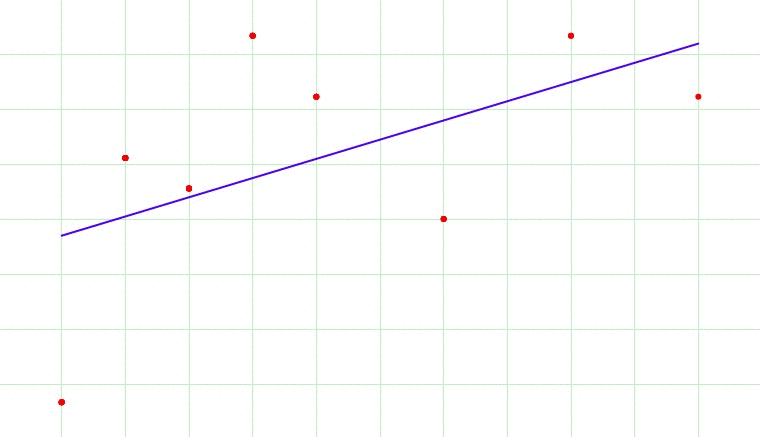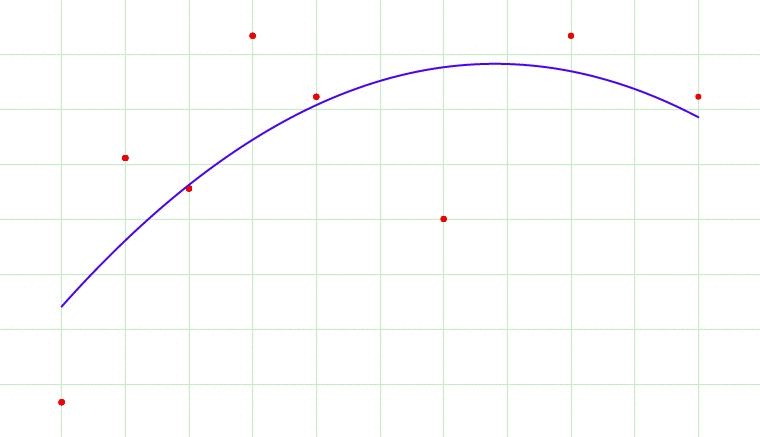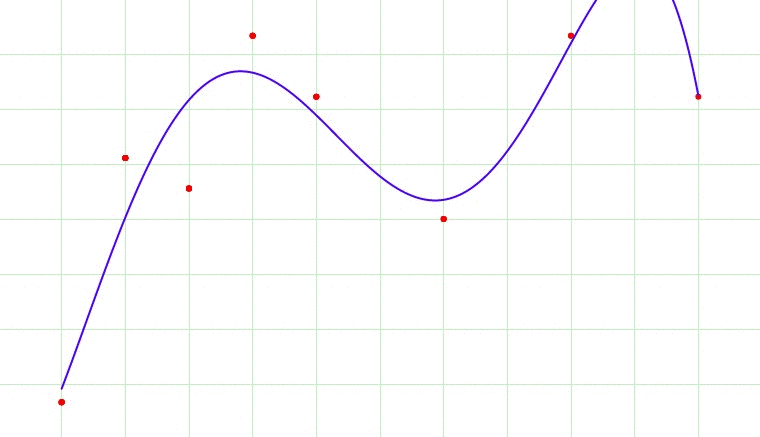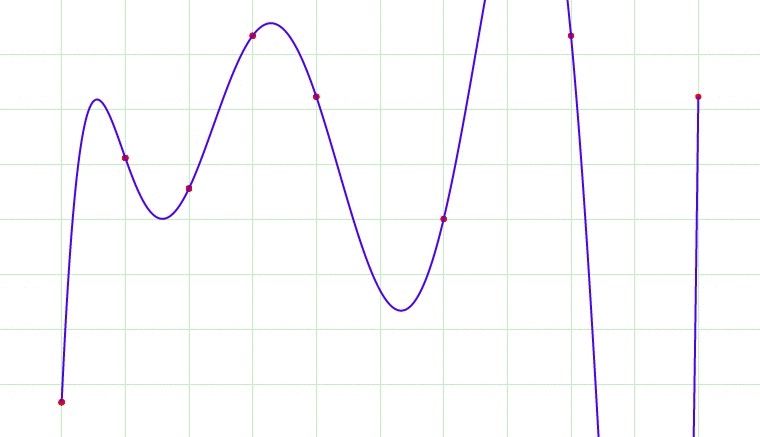
Fig 1. Overfitting?

Overfitting occurs when our model is tuned so closely to our training (i.e., in-sample) dataset, that it is practically useless for forecasting and has poor performance for the test (i.e., out-of-sample) dataset.

Often, when are have a dataset, there is a signal and noise. For our model to be accurate out-of-sample, we want our model to fit the signal and ignore the noise. If we our model overfits the data, it will not be accurate as it fitted for the noise within our in-sample dataset.

Fig 1 cycles through 7 images. Which image would be the most appropriate model fit for the data? The 1st image is a single line through the data and broadly gives us the direction of the data. The 7th image fits through every point in the dataset, and this would lead to overfitting as it would lead us to believe that the next point in the dataset would be a data point that would ascending sharply. Perhaps the best model would be the 2nd or 3rd image. We let an optimally tuned model tell us what is the best.

Regularization

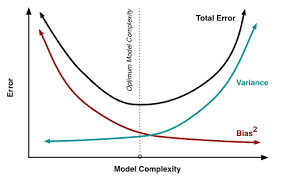
Fig 2. Error vs Model Complexity

As model complexity increases (e.g, in linear regression this is the number of predictors), the model estimates' variance also increases, but the bias decreases (see Fig 2). An unbiased OLS with many predictors would place us on the right side of the Fig 1 which is a sub-optimal solution since the total error and variance is high. We use regularization as a technique to introduce some bias to lower the variance and shift our model towards the left towards optimal model complexity. Regularization is almost always beneficial for the predictive performance of the model and its benefits are intuitively exemplified in Fig 3.

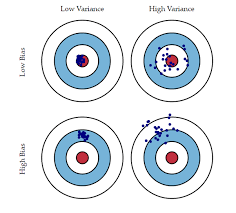
Fig 3. Bias vs Variance

There are three popular regularization techniques, each of them aiming at decreasing the size of the coefficients:

Ridge Regression, which penalizes sum of squared coefficients (L2 penalty).
Lasso Regression, which penalizes the sum of absolute values of the coefficients (L1 penalty).
Elastic Net, a convex combination of Ridge and Lasso.

The regularization parameter is also known as the lambda parameter (\(\lambda\)) and penalizes all parameters except the intercept so that the model generalizes the data and minimizes overfitting. Having (\(\lambda\)) adds an additional penalty parameter to the cost function that can be tuned via cross-validation.

Lasso regression (L1)

Lasso stands for Least Absolute Shrinkage and Selection Operator. It adds the 'absolute value of magnitude' of the coefficient to penalize the loss function.

\begin{equation*} \min_{\Theta} J(\Theta) = \frac{1}{2m} \sum^m_{i=1} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda_{1} \sum^{N}_{j=1} |\Theta_{j}| \end{equation*}

For high values of \(\lambda_{1}\), many coefficients are exactly zeroed under lasso, which is never the case in ridge regression.

Ridge regression (L2)

Ridge regression adds 'squared magnitude' of the coefficient as a penalty term to the loss function.

\begin{equation*} \min_{\Theta} J(\Theta) = \frac{1}{2m} \sum^m_{i=1} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda_{2} \sum^{N}_{j=1} \Theta^2_{j} \end{equation*}

Lasso vs Ridge (L1 vs L2)

Feature selection
- Lasso performs well when a small number of parameters are significant, and the other parameters are close to zero (i.e., few predictors influence the response). Lasso performs sparse selection. It shrinks the less important feature's coefficients to zero and can remove some features altogether. This is useful for feature selection if you have a large number of features in your dataset.
- Ridge performs well when there are many large parameters of about the same value (i.e., many predictors influence the response).
Multi-collinearity
- Lasso, one of the correlated predictors has a larger coefficient, while the others are (nearly) zero-ed (i.e., indifferent to the correlated variables and generally picks one or the other).
- Ridge, performs shrinkage of the two coefficients towards each other (i.e., the coefficients of correlated predictors are similar).
Scaling
- Lasso is not independent of the scaling.
- Ridge is indifferent to multiplicative scaling of the data.
Prediction
- Lasso penalizes coefficients more uniformly.
- Ridge penalizes the largest coefficients more than the smaller ones (due to the squared in the penalty term). In a forecasting problem with a powerful predictor, the predictor's effectiveness might be shrunk by ridge compared to lasso.

Elastic Net

Elastic Net emerged due to the weaknesses of lasso (i.e., variable selection is too dependent on data, unstable model parameterization). Thus, a solution is to combine the penalties of ridge regression and lasso to get the best of both worlds. Elastic Net aims at minimizing the following loss function:

\begin{equation*} \min_{\Theta} J(\Theta) = \frac{1}{2m} \sum^m_{i=1} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda_{1} \sum^{N}_{j=1} |\Theta_{j}| + \lambda_{2} \sum^{N}_{j=1} \Theta^2_{j} \end{equation*}

Elastic Net is a compromise between both L1 and L2 regularization that attempts to shrink and do a sparse selection simultaneously. In most statistical learning and machine learning packages, Elastic Net is implemented as follows:

\begin{equation*} \min_{\Theta} J(\Theta) = \frac{1}{2m} \sum^m_{i=1} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda \left( \alpha \sum^{N}_{j=1} |\Theta_{j}| + \frac{1-\alpha}{2} \sum^{N}_{j=1} \Theta^2_{j} \right) \end{equation*}

The regularization parameter (\(\lambda\)) and mixing parameter (\(\alpha\)) need to be tuned. The mixing parameter is tuned to be between ridge (\(\alpha=0\)) and lasso (\(\alpha=1\)).