Machine learning model peformance metrics

(updated )

Comments

Using the right metrics for our machine learning model and the dataset that is being explored is important. It is particularly important to understand the elements of the confusion matrix as several metrics are calculated based on it. Other popular metrics are the ROC-AUC and log-loss metric

Confusion Matrix

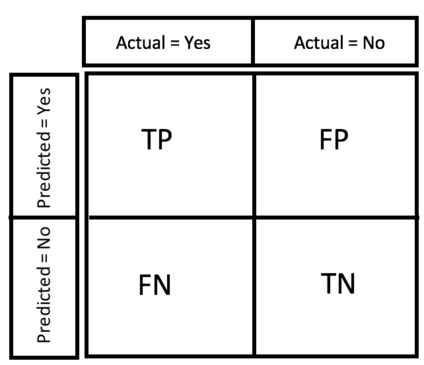
/images/ml/ml_confusion_matrix.png
True Positive (TP)

Number of cases that are predicted as True and are actually True.

True Negative (TN)

Number of cases that are predicted as False and are actually False.

False Positive (FP)

Number of cases are are predicted as True and are actually False.

False Negative (FN)

Number of cases that are predicted as False and are actually True.

Confusion Matrix Metrics

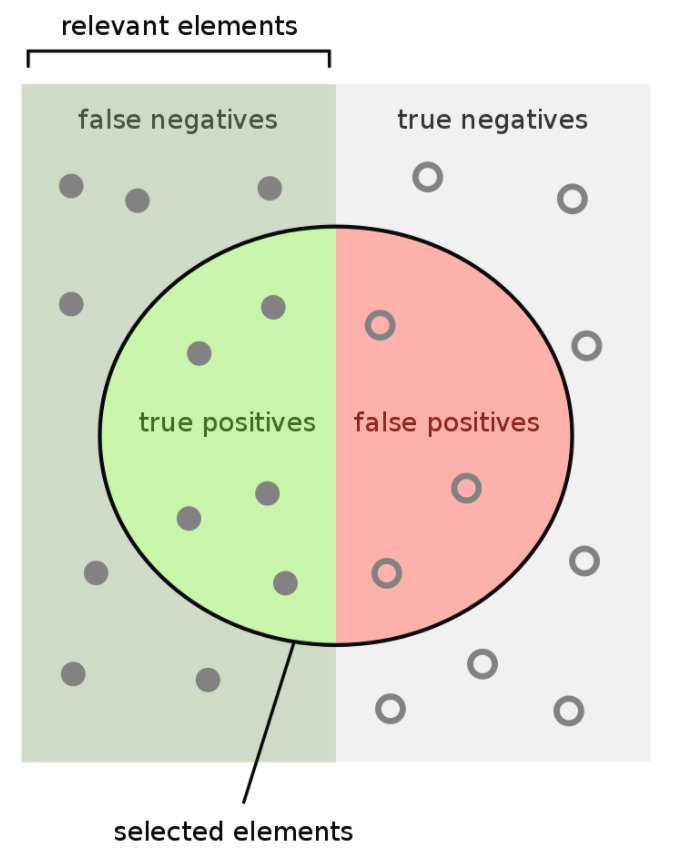
/images/ml/ml_metric_diag.png
Accuracy

Percentage of items classified accurately. \(\frac{TP+TN}{TP+TN+FP+FN}\)

/images/ml/ml_precision_recall.png
Precision (P)

Fraction of predicted positive events that are actually positive (i.e., how correct is the model?). \(\frac{TP}{TP+FP}\)

Sensitivity/True Positive Rate/Recall (R)

Fraction of positives predicted correctly (i.e., what percentage of all positive cases did your model capture accurately?). \(\frac{TP}{TP+FN}\)

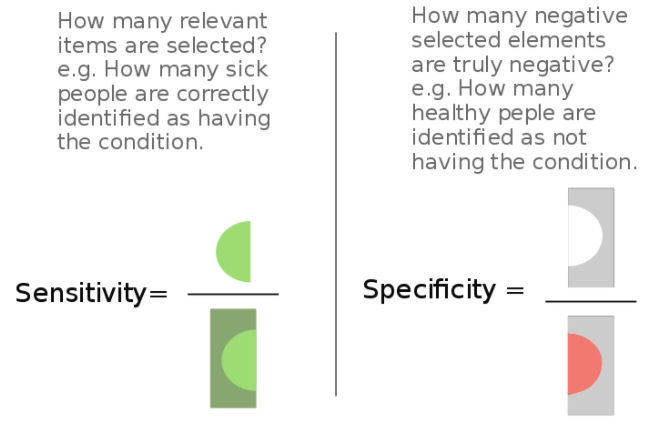
/images/ml/ml_sensitivity_specificity.png
Specificity/True Negative Rate

Number of items correctly identified as negative as a percentage of total true negatives. This is the opposite of Recall. \(\frac{TN}{TN+FP}\)

Type 1 Error/False Positive Rate

Number of items wrongly identified as positive out of total true negatives. \(\frac{FP}{FP+TN}\)

Type II Error/False Negative Rate

Number of items wrongly identified as negative out of total true positives \(\frac{FN}{FN+TP}\)

F1 Score

This is the Harmonic Mean of Precision and Recall. It is a single score that represents both Precision and Recall. \(\frac{2 \times \text{P} \times \text{R}}{\text{P}+\text{R}}\)

Tip

  • Only use Accuracy when target variable classes are balanced (i.e., 80-20). Never use accuracy for imbalanced datasets.

  • Use Precision when it is absolutely necessary that all predicted cases are correct. For example, if it situation is to predict whether a patient needs open-heart surgery, you want to make sure you are correct as being wrong has a high cost (for the patient anyway)

  • Use Recall when it necessary to capture all possibilities that a case is True. For example, if you are identifying patients for quarantine for a highly contagious disease at an airport for an additional 10 minute screening, you would use Recall as the cost of letting the sick patient through is high.

ROC-AUC

Receiver Operating Characteristic - Area under Curve

/images/ml/ml_auc_roc.png

Log-Loss

Log-loss involves the idea of probabilistic confidence for a specific class.

\begin{equation*} \text{LogLoss} =\frac{1}{N} \sum^{N}_{i=1} \sum^{M}_{j=1} y_{ij} \log (p_{ij}) \end{equation*}

\(y_{ij}\), indicates whether sample \(i\) belongs to class \(j\). \(p_{ij}\), indicates the probability of sample \(i\) belonging to class \(j\). Log Loss has no upper bound and it exists on the range \([0, \infty)\). Log Loss nearer to 0 indicates higher accuracy, whereas if the Log Loss is away from 0 then it indicates lower accuracy.

In general, minimising Log Loss gives greater accuracy for the classifier.

Cohen's Kappa metric

Metric that is useful for imbalanced classification

Comments

Comments powered by Disqus